Optimierungsleistung bei synthetischen Gaussian- und Tree-Embeddings
Übersicht der Links
Abstrakt und 1. Einleitung
-
Verwandte Arbeiten
-
Konvexe Relaxationstechniken für Hyperbolische SVMs
3.1 Vorbemerkungen
3.2 Ursprüngliche Formulierung der HSVM
3.3 Semidefinite Formulierung
3.4 Moment-Summe-der-Quadrate-Relaxation
-
Experimente
4.1 Synthetischer Datensatz
4.2 Echter Datensatz
-
Diskussionen, Danksagungen und Referenzen
\
A. Beweise
B. Lösungsextraktion in Relaxierter Formulierung
C. Zur Moment-Summe-der-Quadrate-Relaxationshierarchie
D. Platt-Skalierung [31]
E. Detaillierte Experimentelle Ergebnisse
F. Robuste Hyperbolische Support Vector Machine
4.1 Synthetischer Datensatz
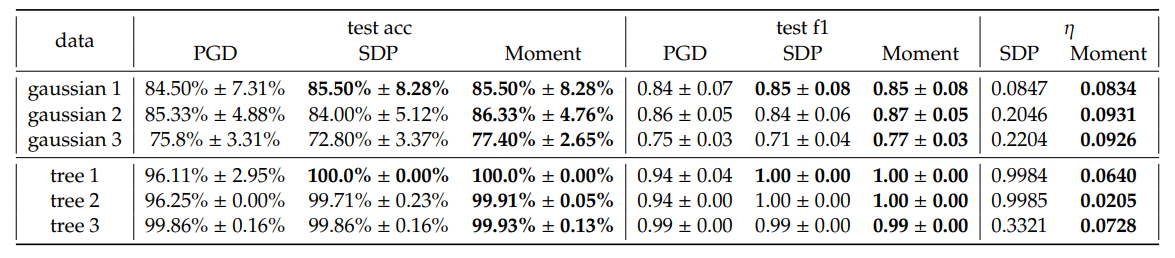
\ Im Allgemeinen beobachten wir einen geringen Anstieg der durchschnittlichen Testgenauigkeit und des gewichteten F1-Scores von SDP und Moment im Vergleich zu PGD. Bemerkenswerterweise zeigt Moment häufig konsistentere Verbesserungen im Vergleich zu SDP über die meisten Konfigurationen hinweg. Darüber hinaus liefert Moment kleinere Optimalitätslücken 𝜂 als SDP. Dies entspricht unserer Erwartung, dass Moment enger als SDP ist.
\ Obwohl Moment in einigen Fällen, beispielsweise wenn 𝐾 = 5, deutlich geringere Verluste im Vergleich zu sowohl PGD als auch SDP erzielt, ist dies im Allgemeinen nicht der Fall. Wir betonen, dass diese Verluste keine direkten Messungen der Generalisierbarkeit der Max-Margin-Hyperbolischen-Separatoren sind; vielmehr sind sie Kombinationen aus Margenmaximierung und Bestrafung für Fehlklassifikation, die mit 𝐶 skaliert. Daher könnte die Beobachtung, dass die Leistung bei der Testgenauigkeit und dem gewichteten F1-Score besser ist, obwohl der unter Verwendung extrahierter Lösungen von SDP und Moment berechnete Verlust manchmal höher ist als der von PGD, auf die komplizierte Verlustlandschaft zurückzuführen sein. Genauer gesagt können die beobachteten Zunahmen des Verlusts auf die Komplexität der Landschaft und nicht auf die Wirksamkeit der Optimierungsmethoden zurückgeführt werden. Basierend auf den Genauigkeits- und F1-Score-Ergebnissen identifizieren die SDP- und Moment-Methoden empirisch Lösungen, die besser generalisieren als solche, die allein durch Ausführen des Gradientenabstiegs erhalten werden. Wir stellen eine detailliertere Analyse der Auswirkungen von Hyperparametern in Anhang E.2 und der Laufzeit in Tabelle 4 bereit. Die Entscheidungsgrenze für Gaussian 1 ist in Abbildung 5 visualisiert.
\ ![Abbildung 3: Drei Synthetische Gaussians (obere Reihe) und Drei Baum-Einbettungen (untere Reihe). Alle Merkmale befinden sich in H2, werden aber durch stereographische Projektion auf B2 visualisiert. Verschiedene Farben repräsentieren verschiedene Klassen. Für den Baumdatensatz werden die Graphenverbindungen ebenfalls visualisiert, aber nicht im Training verwendet. Die ausgewählten Baum-Einbettungen stammen direkt von Mishne et al. [6].](https://cdn.hackernoon.com/images/null-yv132j7.png)
\ Synthetische Baum-Einbettung. Da hyperbolische Räume gut für die Einbettung von Bäumen geeignet sind, generieren wir zufällige Baumgraphen und betten sie in H2 ein, wobei wir Mishne et al. [6] folgen. Insbesondere kennzeichnen wir Knoten als positiv, wenn sie Kinder eines bestimmten Knotens sind, und andernfalls als negativ. Unsere Modelle werden dann für die Teilbaumklassifikation evaluiert, mit dem Ziel, eine Grenze zu identifizieren, die alle Kindknoten innerhalb desselben Teilbaums umfasst. Eine solche Aufgabe hat verschiedene praktische Anwendungen. Wenn der Baum beispielsweise eine Menge von Tokens darstellt, kann die Entscheidungsgrenze semantische Bereiche im hyperbolischen Raum hervorheben, die den Teilbäumen des Datengraphen entsprechen. Wir betonen, dass ein gemeinsames Merkmal bei solchen Teilbaumklassifikationsaufgaben die Datenunausgeglichenheit ist, die normalerweise zu schlechter Generalisierbarkeit führt. Daher beabsichtigen wir, diese Aufgabe zu verwenden, um die Leistung unserer Methoden unter dieser herausfordernden Einstellung zu bewerten. Drei Einbettungen werden ausgewählt und in Abbildung 3 visualisiert, und die Leistung ist in Tabelle 1 zusammengefasst. Die Laufzeit der ausgewählten Bäume findet sich in Tabelle 4. Die Entscheidungsgrenze von Baum 2 ist in Abbildung 6 visualisiert.
\ Ähnlich wie bei den Ergebnissen der synthetischen Gaussian-Datensätze beobachten wir eine bessere Leistung von SDP und Moment im Vergleich zu PGD, und aufgrund der Datenunausgeglichenheit, mit der GD-Methoden typischerweise zu kämpfen haben, erzielen wir in diesem Fall einen größeren Gewinn beim gewichteten F1-Score. Darüber hinaus beobachten wir große Optimalitätslücken für SDP, aber eine sehr enge Lücke für Moment, was die Optimalität von Moment selbst bei schwerer Klassenunausgeglichenheit bestätigt.
\ 
\
:::info Autoren:
(1) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA ([email protected]);
(2) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA ([email protected]);
(3) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, und Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA ([email protected]).
:::
:::info Dieses Papier ist auf arxiv verfügbar unter CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International) Lizenz.
:::
\
Das könnte Ihnen auch gefallen

Frustabend in der Europa League: Deniz Undav macht VfB-Mitspielern eine harte Ansage

"Kuba wird nicht überleben": Trump kündigt Sekundärzölle gegen Öllieferanten der Insel an