Desempenho de Otimização em Embeddings Gaussianos Sintéticos e de Árvore
Tabela de Links
Resumo e 1. Introdução
-
Trabalhos Relacionados
-
Técnicas de Relaxamento Convexo para SVMs Hiperbólicos
3.1 Preliminares
3.2 Formulação Original do HSVM
3.3 Formulação Semidefinida
3.4 Relaxamento Momento-Soma-de-Quadrados
-
Experiências
4.1 Conjunto de Dados Sintético
4.2 Conjunto de Dados Real
-
Discussões, Agradecimentos e Referências
\
A. Provas
B. Extração de Solução em Formulação Relaxada
C. Sobre Hierarquia de Relaxamento Momento Soma-de-Quadrados
D. Escalonamento de Platt [31]
E. Resultados Experimentais Detalhados
F. Máquina de Vetores de Suporte Hiperbólica Robusta
4.1 Conjunto de Dados Sintético
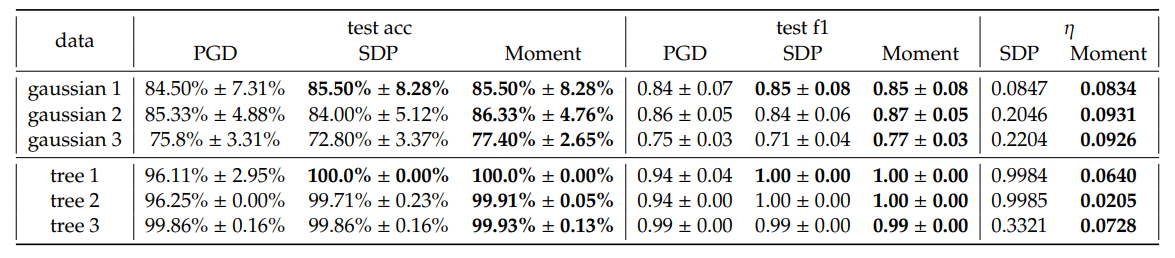
\ Em geral, observamos um pequeno ganho na precisão média de teste e pontuação F1 ponderada do SDP e Moment em relação ao PGD. Notavelmente, observamos que o Moment frequentemente mostra melhorias mais consistentes em comparação com o SDP, na maioria das configurações. Além disso, o Moment apresenta intervalos de otimalidade 𝜂 menores do que o SDP. Isto corresponde à nossa expectativa de que o Moment é mais restrito do que o SDP.
\ Embora em alguns casos, por exemplo quando 𝐾 = 5, o Moment alcance perdas significativamente menores em comparação com o PGD e o SDP, geralmente não é o caso. Enfatizamos que estas perdas não são medidas diretas da capacidade de generalização dos separadores hiperbólicos de margem máxima; pelo contrário, são combinações de maximização de margem e penalização por classificação incorreta que escala com 𝐶. Portanto, a observação de que o desempenho na precisão de teste e pontuação F1 ponderada é melhor, embora a perda calculada usando soluções extraídas do SDP e Moment seja por vezes maior do que a do PGD, pode dever-se à complexa paisagem de perda. Mais especificamente, os aumentos observados na perda podem ser atribuídos às complexidades da paisagem e não à eficácia dos métodos de otimização. Com base nos resultados de precisão e pontuação F1, empiricamente os métodos SDP e Moment identificam soluções que generalizam melhor do que aquelas obtidas executando apenas descida de inclinação. Fornecemos uma análise mais detalhada sobre o efeito dos hiperparâmetros no Apêndice E.2 e tempo de execução na Tabela 4. O limite de decisão para Gaussiano 1 é visualizado na Figura 5.
\ ![Figura 3: Três Gaussianos Sintéticos (linha superior) e Três Incorporações de Árvore (linha inferior). Todas as características estão em H2 mas visualizadas através de projeção estereográfica em B2. Cores diferentes representam classes diferentes. Para o conjunto de dados de árvore, as conexões gráficas também são visualizadas mas não usadas no treino. As incorporações de árvore selecionadas vêm diretamente de Mishne et al. [6].](https://cdn.hackernoon.com/images/null-yv132j7.png)
\ Incorporação de Árvore Sintética. Como os espaços hiperbólicos são adequados para incorporar árvores, geramos gráficos de árvore aleatórios e incorporamo-los em H2 seguindo Mishne et al. [6]. Especificamente, rotulamos nós como positivos se forem filhos de um nó especificado e negativos caso contrário. Os nossos modelos são então avaliados para classificação de subárvore, visando identificar um limite que inclua todos os nós filhos dentro da mesma subárvore. Tal tarefa tem várias aplicações práticas. Por exemplo, se a árvore representa um conjunto de tokens, o limite de decisão pode destacar regiões semânticas no espaço hiperbólico que correspondem às subárvores do gráfico de dados. Enfatizamos que uma característica comum em tal tarefa de classificação de subárvore é o desequilíbrio de dados, que geralmente leva a uma fraca capacidade de generalização. Portanto, pretendemos usar esta tarefa para avaliar o desempenho dos nossos métodos neste cenário desafiante. Três incorporações são selecionadas e visualizadas na Figura 3 e o desempenho é resumido na Tabela 1. O tempo de execução das árvores selecionadas pode ser encontrado na Tabela 4. O limite de decisão da árvore 2 é visualizado na Figura 6.
\ Semelhante aos resultados dos conjuntos de dados Gaussianos sintéticos, observamos melhor desempenho do SDP e Moment em comparação com o PGD, e devido ao desequilíbrio de dados com que os métodos GD normalmente têm dificuldade, temos um ganho maior na pontuação F1 ponderada neste caso. Além disso, observamos grandes intervalos de otimalidade para o SDP, mas intervalo muito restrito para o Moment, certificando a otimalidade do Moment mesmo quando o desequilíbrio de classe é severo.
\ 
\
:::info Autores:
(1) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA ([email protected]);
(2) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA ([email protected]);
(3) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, e Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA ([email protected]).
:::
:::info Este artigo está disponível no arxiv sob licença CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International).
:::
\
Você também pode gostar

IG Group hoàn tất mua lại Independent Reserve, mở rộng mảng crypto

O Que os Fluxos de ETF e os Dados da Binance Indicam Sobre a Liquidez Atual do Bitcoin
